Operaciones con matrices - Algebra
Suma y resta de matrices
Sean A y B dos matrices m x n. Entonces la suma/resta de A y B denotado por A ± B está dada por:
Ejemplo
Tenemos los siguientes vectores:
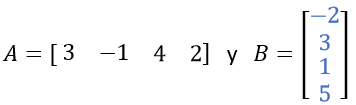
Para obtener la suma o restan, respetamos el orden de los términos: el primero con el primero, el segundo con el segundo, el tercero con el tercero, etc.
Hacemos la suma de dichas matrices:
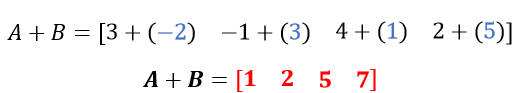
Multiplicación por un escalar
Si A es una matriz de m x n y α es un escalar, entonces la matriz αA está dada por:
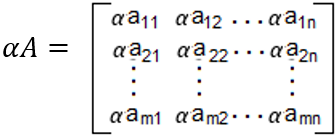
Ejemplo
Tenemos la siguiente matriz, la cual multiplicaremos por α=3.
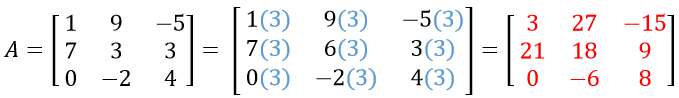
Multiplicación de matrices
Sea A una matriz m x n y B una matriz de q x p, entonces el producto de A y B es una matriz de m x p y se denota por:
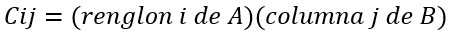
Ejemplo
Tenemos las matrices:
Para resolver la multiplicación se debe checar que n y q sean iguales, si lo son, se procede a multiplicar y el resultado será una matriz de m x p:
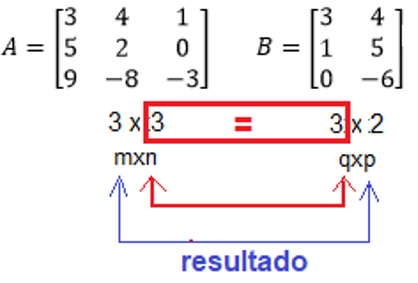
Para multiplicar, se sigue la fórmula vista arriba: renglón i de A por columna j de B:
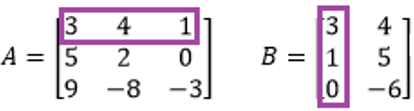
Cada término multiplicado se sumará y se pondrá en su lugar correspondiente siguiendo el siguiente orden:
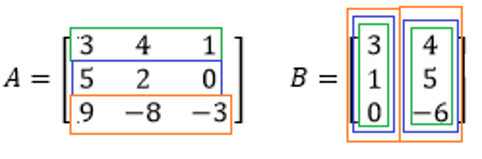
Para facilitar su entendimiento, multiplicamos color por color y se ordena igual, por color:
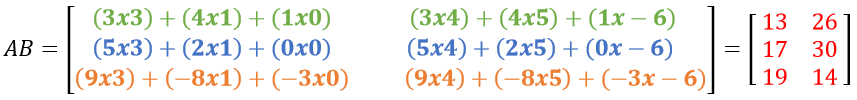
Ejercicios
Resultados
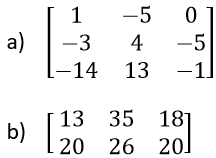
Introducción a Vectores y Matrices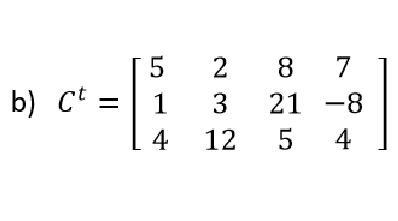
Transpuesta de una matriz
Muy bn entendido