Representación polar y trigonométrica de números complejos - Algebra
Introducción
Como se mencionó en artículos anteriores, los números complejos se pueden representar de las siguientes maneras: rectangular, polar y también la llamada trigonométrica. En este caso explicaremos la segunda y tercera.
Marco teórico
La representación polar de un numero complejo es por un módulo |Z| y un argumento Θ como subíndice.
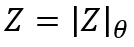
Y la representación trigonométrica es la siguiente:
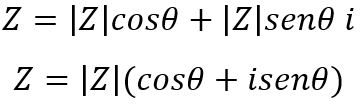
En el plano, podemos observarlo de esta manera:
Donde, a es la parte real y b es la parte imaginaria en forma rectangular y |Z| y Θ es en la forma polar.
Para poder transformar un número complejo representado rectangularmente a uno polar se requieren las siguientes fórmulas:
Y se acomodan los valores de la siguiente manera:
Para poder transformar un número complejo representado rectangularmente a uno trigonométrico se requieren las mismas fórmulas:
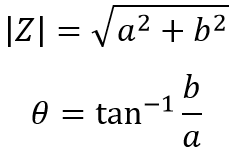
Y se acomodan los valores de la siguiente manera:
Para transformar de una forma trigonométrica o polar a rectangular se utilizan las mismas ecuaciones, pues como sabemos en ambos métodos se tiene |Z| y Θ. Las ecuaciones son las siguientes:
Y se acomodan los valores de la siguiente manera:
Para este caso no es necesario utilizar ninguna ecuación, pues como sabemos en ambos métodos se tiene |Z| y Θ, por lo que teniendo esos valores, solo es cuestión de acomodarlos en la forma que nosotros queremos.
Trigonométrica:
Polar:
Ejemplos
Tenemos el valor rectangular:
Para transformar a polar y trigonométrica, se procede a obtener el valor del módulo y del argumento:
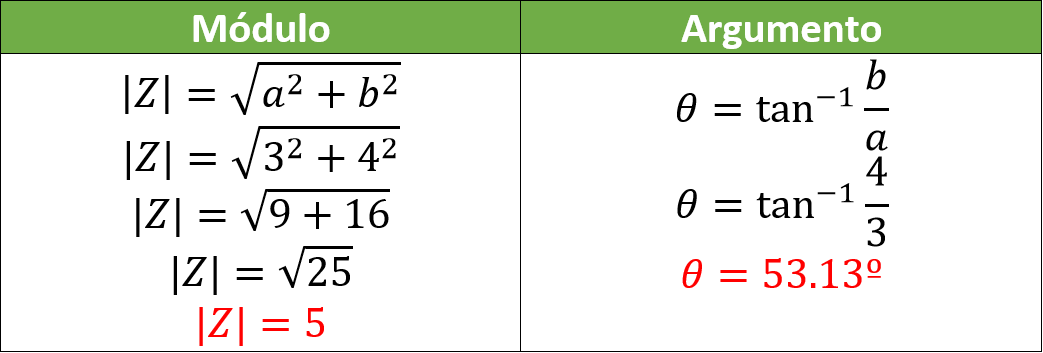
Por lo tanto el resultado en forma polar es:
Y el resultado en forma trigonométrica es:
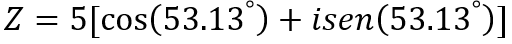
Ejercicios
Realizar las siguientes transformaciones de rectangular a polar y trigonométrica.
Realizar las siguientes transformaciones a su forma rectangular.
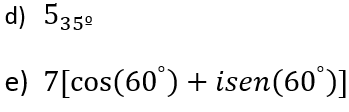
Resultados
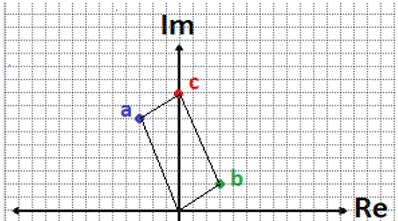Sumas y restas en el plano - Ley del paralelogramo
Multiplicación y división de números complejos en forma polar