PUBLICIDAD
Teorema del residuo - Algebra
Marco teórico
El teorema del residuo establece que: “si un polinomio de X f(x) se divide entre (x-a), donde a es un número cualquiera, entonces el residuo será el resultado de f(a)”. Este teorema nos ayuda a verificar si el resultado de una división de polinomios está correcta.
EJEMPLO
Tenemos la siguiente división:
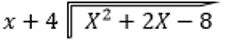
Realizamos la división como aprendimos en la primaria, pero con la diferencia que utilizaremos álgebra:
- Buscamos un cociente que al multiplicarlo por la x de (x+4) nos dé X², en este caso será x.
- Multiplicamos el cociente x por el divisor (x+4) y restaremos el valor a la primer parte de la dividendo (X²+2X).
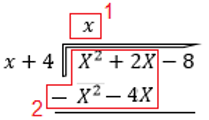
- Resolvemos la resta y bajamos el -8 (como nos enseñaron en primaria)
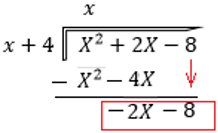
- Ahora buscamos otro valor para el cociente que, al multiplicarlo por x+4 nos eliminé el valor de (-2X) y nos resulte un solo número de residuo, en este caso será 2 (recordemos que el signo nos lo dará el valor que queremos eliminar de acuerdo a la ley de los signos)

Publicidad
- Se realiza la resta y obtenemos el residuo que en este caso es 0
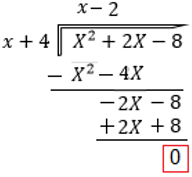
- Se comprueba la división con el teorema del residuo obteniendo el valor de X al igualar a cero la ecuación X+4
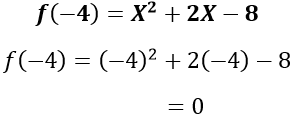
Agregar comentario

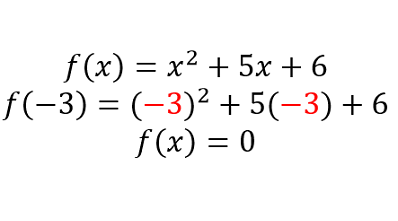 Teoría de Polinomios
Teoría de Polinomios División sintética
División sintética
Cómo se haría si estuviera divido entre tres cifras