Regla de Cramer - Algebra
Marco teórico
Este método para obtener determinantes es muy útil a la hora de resolver sistemas de ecuaciones lineales del tipo Ax=b donde A es una matriz nxn y el determinante de A diferente a 0 está dada por
Donde Di es el determinante de una matriz menor que resulta del intercambio de la columna resultado por cada una de las columnas original.
Se tiene el siguiente sistema de ecuaciones:
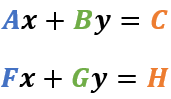
Para obtener los valores de X y Y se resolverán las determinantes D, D1 y D2.
D se obtiene de colocar en matriz los valores de X y Y:
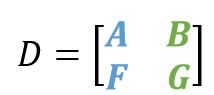
D1 se obtiene intercambiando la primera columna por la columna de resultados:
D2 se obtiene intercambiando la segunda columna por la columna de resultados:
Ya que se tienen las determinantes de las matrices anteriores (por el método que más les convenga de los vistos anteriormente), se utilizan dichos valores para finalmente resolver el sistema de ecuaciones X y Y utilizando la fórmula vista al inicio de este artículo:
Ejemplo
Se tiene el siguiente sistema de ecuaciones lineales:
La matriz D es:
NOTA: Las determinantes de cada matriz no se resolverán paso a paso para sintetizar el procedimiento, pero pueden usar cualquier método de los que ya hemos visto.
La matriz D1 es:
La matriz D2 es:
La matriz D3 es:
Ahora para resolver el sistema de ecuaciones usamos la fórmula:
Ejercicios
Resultados
Método de matriz triangular - Determinante de una matriz
Me gusta estés sistema de desarrollo matemático 3x3 y 2x2