Método de matriz triangular - Determinante de una matriz - Algebra
Introducción
Anteriormente vimos dos métodos para obtener la determinante de una matriz, en este caso se mostrará un tercer método llamado matriz triangular.
Marco teórico
Se le conoce así ya que se va resolviendo de manera que se coloquen ceros formando un triángulo, la orientación de dicho triangulo ya sea inferior (triangulo amarillo) o superior (triangulo rojo) se determinará principalmente por el área donde ya se tenga un cero. Si la matriz no tiene ninguno, se puede iniciar por la orientación de su preferencia.
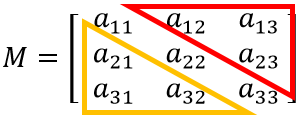
En este método los cálculos a realizar son sencillos, pero se debe estar concentrado para no perder el orden que se lleva, ya que se debe aplicar una operación a todo el renglón para ir convirtiendo el triángulo de ceros, finalmente obtener la determinante, simplemente se multiplican los números colocados fuera de la diagonal o hipotenusa del triángulo.
IMPORTANTE: no se puede multiplicar por cero, y se debe tomar en cuenta desde el primer renglón hasta el último renglón.
A continuación se dará un ejemplo explicado paso a paso para comprender mejor este tema.
Ejemplo
Se tiene la matriz:
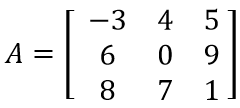
Como no tiene un cero en ninguna de las esquinas se puede empezar por la parte superior o inferior. En este caso usaremos la inferior, por lo tanto empezaremos del segundo renglón.
Para empezar la conversión, se debe pensar en una fórmula donde el 6 se convierta en 0 utilizando los renglones.
Y para no perdernos, haremos las operaciones por columna con su color correspondiente acomodados en la siguiente tabla (la cual es opcional, aquí se coloca a manera de explicación y orden):
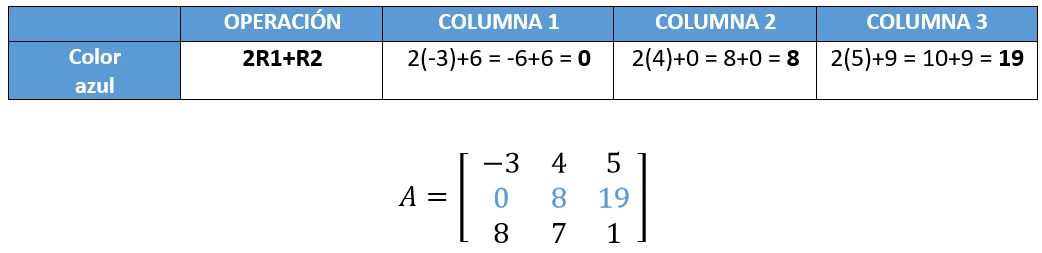
Ahora, buscamos una operación que al realizarla, nos convierta el 8 del tercer renglón a 0:
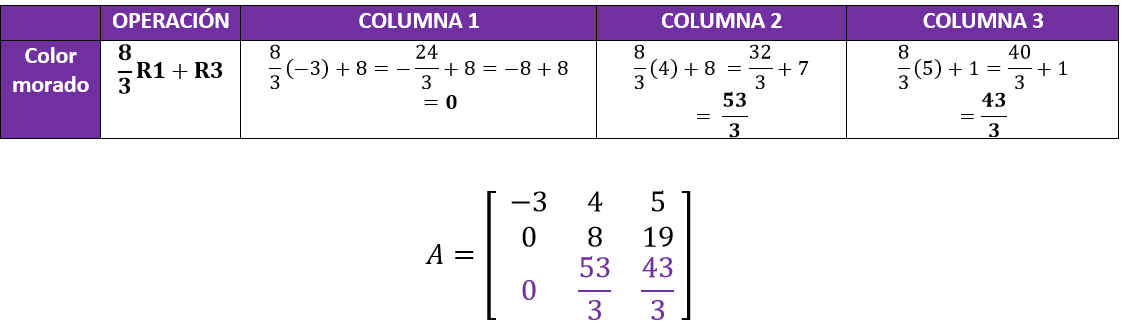
Ya tenemos los primeros dos ceros de nuestro triangulo, falta uno para completarlo. Ahora bien, debemos buscar una operación que nos convierta en cero el 53/3 contemplando solo el renglón 2, esto porque ya tiene un cero al inicio. Por lo tanto, usaremos:
NOTA: el -53/24 lo obtuvimos de dividir 53/3 entre 8. Esto para encontrar el número que multiplicado por 8 diera como resultado los 53/3.
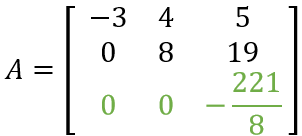
El resultado de la determinante será la multiplicación de la diagonal resultante o hipotenusa del triángulo, en este caso:
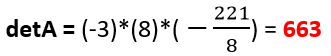
Ejercicios
Resultados
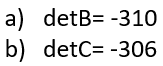
Método de la primera línea - Determinante de una matriz
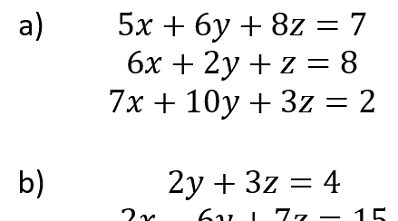Regla de Cramer