Teoría de números complejos - Algebra
Los números complejos se componen de una parte real y otra imaginaria, lo cual hace que incluyan todas las raíces de los polinomios a diferencia de los números reales.
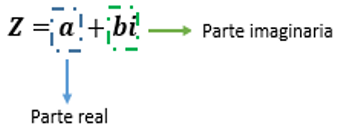
Para comprender mejor lo que son los números imaginarios, tenemos el siguiente ejemplo:
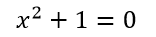
Para despejar X de la ecuación se realiza el siguiente desarrollo:
Como podemos observar, X es igual a la raíz de un número negativo, en este caso -1. Y si intentamos sacarle raíz a un número negativo nuestra calculadora marcará error ya que eso no es posible, por lo tanto se dice que la raíz de un número negativo es un número imaginario.
Dicho lo anterior, si tenemos un número indicado como ' ni ' significa que n es el valor que multiplica a la raíz del número negativo, por ejemplo:
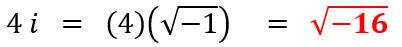
Para graficar un número complejo se tiene un sistema de coordenadas compuesta por la parte real (eje de las X) y la parte imaginaria (eje de las Y), a continuación se tienen unos ejemplos:
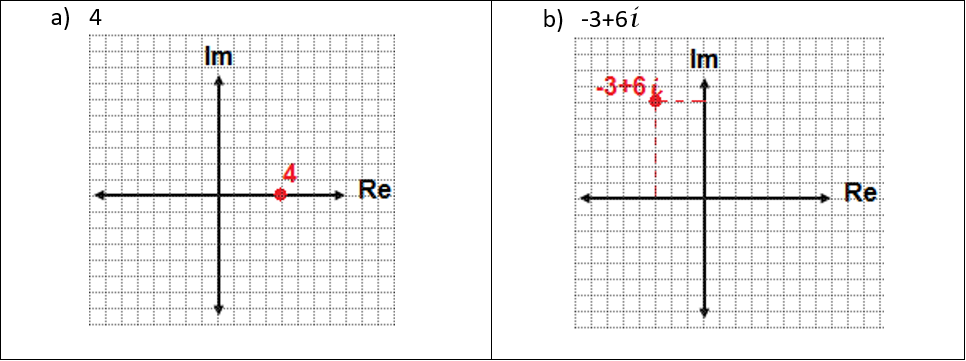
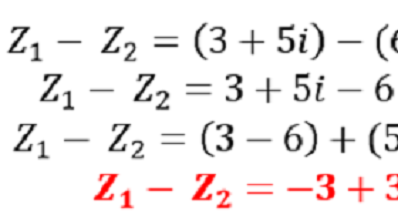Sumas y restas con números complejos
Me gusta
Lo mejor que el hombre debe aprender es la matematica
Me gusta la matemática y es mi encanto.
Mi encanto es la matemática
Me gusta la matemática