Leyes de Kirchhoff - Circuitos
Introducción
Aunque la ley de Ohm es muy útil para el análisis de circuitos y es una de las más utilizadas, hay otro conjunto de leyes que nos ayudarán a resolver circuitos más complejos. En este artículo te explicaremos que son las leyes de Kirchhoff, y como utilizarlas al momento de analizar circuito.
Existen 2 leyes de Kirchhoff que son:
- Ley de corriente de Kirchhoff (LCK)
- Ley de tensión de Kirchhoff (LTK)
Ley de corriente de Kirchhoff (LCK)
La primera ley de Kirchhoff (Ley de corrientes) nos dice que la suma algebraica de las corrientes que entran a un mismo nodo es igual a cero.
Por consecuencia, las corrientes que entran a un mismo nodo deben de dar el mismo valor que las corrientes que salen del nodo. Si lo proponemos matemáticamente, cuando una corriente entra a un nodo esta tendrá un valor positivo (+), y cuando una corriente sale del nodo esta tendrá un valor negativo (-).
Gráficamente y matemáticamente lo podemos ver de la siguiente manera:
Por lo tanto:
Ley de tensión de Kirchhoff (LTK)
La segunda ley de Kirchhoff (Ley de voltajes) nos dice que la suma algebraica de voltajes en una trayectoria cerrada (lazo o malla) de un circuito es igual a cero. Por consecuencia, la suma de voltajes aportados debe ser lo mismo que la suma de caídas de tensión en una malla/lazo.
Si seguimos la convención pasiva de los signos, la ecuación matemática quedaría de la siguiente manera:
Por lo tanto:
Ejercicio
Utilizando LCK, LVK y ley de Ohm, determine el valor de i1, i2, i3 tomando en cuenta que i4 = 7.8mA. Además obtenga el voltaje de V1, V2, V3 y V4.
Basándonos en la ley de corrientes de Kirchhoff tenemos que la ecuación matemática para:
Nodo B:
i1 + i3 = i2
Nodo C:
i4 + i3 =10 mA
Para la ecuación del Nodo C como sabemos que i4 = 7.8mA tenemos que:
i3 =10 mA – 7.8 mA
i3 =2.2 mA
Ahora con la ley de Ohm, podemos obtener el voltaje “V2”:
V2 = 100Ω * 2.2 mA
V2 = 0.22 V
Y también podemos obtener el voltaje “V4”:
V4 = 480Ω * 7.8 mA
V4 = 3.74 V
Basándonos en LVK podemos obtener el voltaje “V3” si analizamos el lazo “B-C-D”:
V3 = V4 – V2
V3 = 3.74 V – 0.22 V
V3 = 3.52 V
Habiendo obtenido el voltaje “V3” podemos obtener la corriente “i2” por ley de Ohm:
i2 = 3.52 V / 330 Ω
i2 = 10.66 mA
Y ahora con esa corriente, podemos usar la LCK aplicándola en el nodo B para obtener i1. Con la ecuación obtenida al inicio del ejercicio:
i1 = i2 – i3
i1 = 10.66 mA – 2.2 mA
i1 = 8.46 mA
Finalmente solo nos queda obtener el voltaje “V1”, utilizando LVK en la trayectoria “A-B-E” nos queda:
V1 = 12V – V3
V1 = 12V – 3.52V
V1 = 8.48 V
Quedando finalmente:
i2 = 10.66 mA
i3 = 2.2 mA
i4 = 7.8 mA
V1 = 8.48 V
V2 = 0.22 V
V3 = 3.52 V
V4 = 3.74 V
Ramas, nodos, lazos y mallas
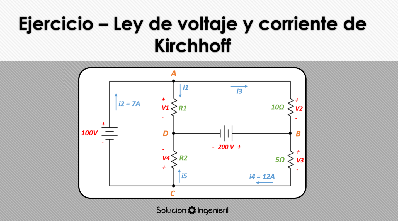Ejercicio – Ley de voltaje y corriente de Kirchhoff 