Multiplicación con números complejos - Algebra
Marco teórico
La multiplicación es muy fácil y muy requerida a la hora de realizar operaciones matemáticas, por lo que también se puede realizar con números complejos. Sin embargo, aunque el fin de ellas es el mismo (obtener un producto de dos números) la metodología para realizarlas es un poco distinta. Si tenemos:
Y tenemos:
Entonces al multiplicarlos, debemos recordar el orden de multiplicación de los polinomios, dónde primero se multiplica la parte real, luego la parte imaginaria y luego la real con la imaginaria:
Como podemos observar, tenemos una parte con una i² , recordando un poco la teoría de números complejos (que podrá observar en publicaciones anteriores) el valor i=√-1, por lo tanto, las leyes de los exponentes nos dicen que si tenemos una raíz cuadrada elevada a un exponente cuadrado, ambas desaparecen:
Entonces:
Ejemplos
Tenemos las siguientes ecuaciones:
Para multiplicarlas hacemos lo siguiente:
Ejercicios
Realizar los siguientes ejercicios de acuerdo a los ejemplos anteriores:
Resultados
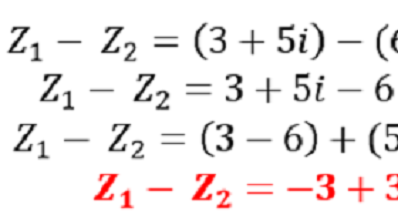Sumas y restas con números complejos
División de números complejos
SARA SE HACE ASI:
(7+5i)*(7+5i)
Y la e?
Como se hace la c
Y ¿cómo se resuelve la D?
Hola Jean
Esperemos nos demos a explicar como se resuelve
(3 + 5i)(5 + 7i)(2-i)
(15 + 21i + 25i + 35i^2)(2-i)
(15 + 46i – 35)(2-i)
(-20 + 46i)(2-i)
-40 + 20i + 92i – 46i^2
-40 + 112i + 46
6 + 112i
Saludoooos!